Haskell 是一个强类型语言

类型与数据

常见类型

• Bool ：两个值 True False ，逻辑非是 not

  Haskell 中约定类型的名字与该类型的数据（类型构造器）的首字母要大写

• Char ：使用单引号，还可以使用反斜杠与 ASCII 码的值的组合来表示一个字符（十进制）

• 整数

  • Int：有符号，范围与系统位数有关。$−2^{31}∼2^{31}−1$ 或 $−2^{63}∼2^{63}−1$

  • Word：无符号，范围与系统位数有关。需导入模块 :m +Data.Word

  • Integer ：任意精度整数，考虑到性能，非必要不使用

  • 在 Data.Int 及Data.Word模块中，Haskell 还支持 Int8、Int16、Int32和 Int64 及对应Word 数

  • 整数字面量：0b、0o 和 0x

    启用二进制需使用 {-# LANGUAGE BinaryLiterals #-} GHC Pragmas(预处理指令)，功能: 设定编译器的状态或者是指示编译器完成一些特定的动作

• 浮点数与小数

  • Float 、 Double
  • Rational ：两个任意精度整数的比 4.1332::Rational = 10333 % 2500

• 字符串： String = [Char]

• 元组：(a,b) ，元组的元件个数和类型变不了；fst ， snd 只用于二元元组

• 函数： T1 -> T2

柯里化

柯里化函数：curry

> :t curry
curry :: ((a, b) -> c) -> a -> b -> c

非柯里化函数：uncurry

> :t uncurry
uncurry :: (a -> b -> c) -> (a, b) -> c

多态函数

一个函数的某个参数可以是任何类型的值，那么这个函数就是多态函数（polymorphic function）

比如

> :t fst
fst :: (a, b) -> a
-- 使用小写字母表示任意类型

> :t length
length :: Foldable t => t a -> Int
-- ad-hoc polymorphism 使用 Typeclass 约束参数

类型类

和 Interface 和 Trait 有点像

有可能有多种类型的字面值 称为 重载的字面值（overloaded literals），比如小数（单双精度），"abc"（字符串或者 字节字符串（ByteString）python2）

重载函数：重载函数的意思是同一个名字的函数可以根据类型或者参数数量的不同有不同的实现。

Haskell 中 参数类型可以重载而参数数量不能（默认的 curry 说明只能用一个参数）（但是我们可以实现可变参数的函数）

类型的别名

type RGB = (Int,Int,Int)

类型类

• Eq ：定义 == 或 /=（Équivalence）

• Ord：定义 <=，依赖于 Eq （Partiellement ordonné）

• Enum：使用 .. 枚举，实现 succ 和 pred 函数

• Bounded： minBound :: a 和 maxBound :: a

• Show ：显示，函数没有其实现，需导入Text.Show.Function

Num

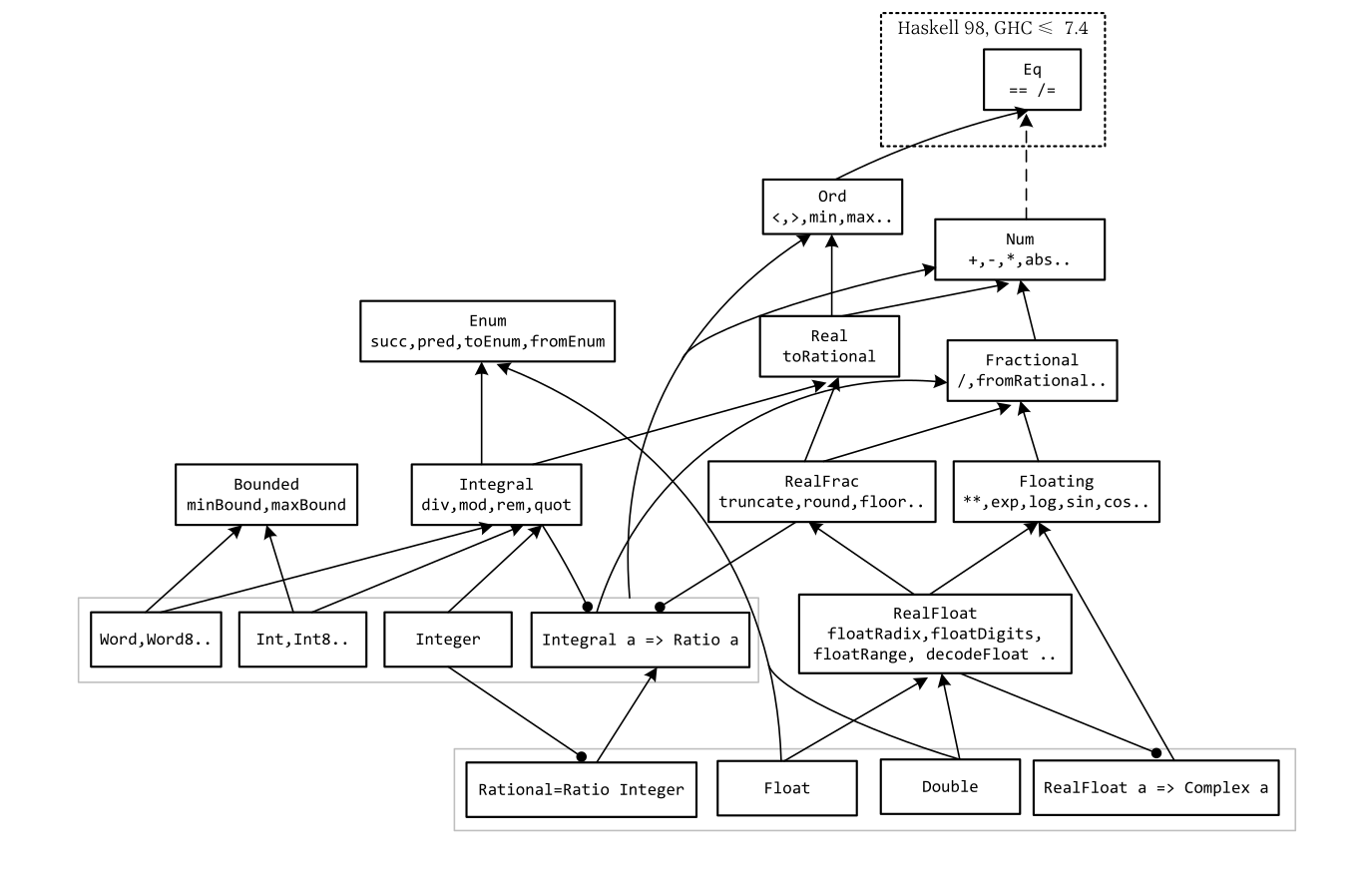
• 复数：Data.Complex (5:+5) + (1:+1)

• 一些数类型相等性的比较是不可判定的

• Float 与 Double 两个小数类型实际是 Enum 类型类，可以使用固定的差值遍历

• 类型转换

  • fromXXX

  • toXXX

  Integral 类型类 包含 Int、Integer、Word

• NaN 与⽆穷⼤

> 0/0
NaN
> 0/0 == 0/0
False --NaN 不与任何数相等，使用`isNaN` 判断
> 1/0
Infinity
> -1/0
-Infinity --可以使用`isInfinite`判断

这两个值无法直接使用，可以导入 ieee754 库，启用 Numeric.IEEE 模块

涉及NaN 的比较大小需要使用 minNum 与 maxNum

• 实数计算可以使用Data.Number.CReal
• 可以使用科学计数法 3.14159e6，启用拓展NumDecimals整数会限定到Num，否则Fractional

函数

变量的值是不变的

> :t (5+)
(5+) :: Num a => a -> a
-- -> 是向右结合的符号

给出一部分参数叫作 偏函数调用（partial application）

函数的定义

i :: Int
i = 1
-- 可以在同一行签名
add, sub :: Int -> Int -> Int
add a b = a + b
sub a b = a - b
-- 多个类型类限定使用括号
fn (Show a, Ord a) => a -> a -> a

函数名不能用大写字母或数字开头

$\lambda$ 表达式

f' :: Num a => a -> a -> a
f' = \x -> \y -> 4*x + 5*y + 1

具体定义和函数签名很好地对应起来

参数之间的箭头可以省略为

f'= \x y -> 4*x + 5*y + 1
g'= \w x y z -> w + y * x - z

• $\alpha$ 替换、$\beta$ 化简、$\eta$ 化简
• 可视化

参数的绑定